Articolo tratto dalla conferenza interna del 9 dicembre 2005, aggiornata ed arricchita
Il moto dei pianeti
Il moto di rivoluzione
[figura 1 – il moto di rivoluzione]
Tutti i pianeti si muovono intorno al sole su orbite ellittiche; moto detto di rivoluzione.
Queste le caratteristiche del moto di rivoluzione:
a) le orbite sono pressoché complanari
b) il moto avviene in senso antiorario
c) il piano dell’orbita terrestre si chiama eclittica e costituisce il riferimento
Il concetto di anno nasce dal tempo impiegato a compiere un giro intorno al sole.
Il moto di rotazione
[figura 2 – il moto di rotazione]
Tutti i pianeti ruotano anche su se stessi; moto detto di rotazione.
Queste le caratteristiche del moto di rotazione:
a) l’asse di rotazione è più o meno inclinato rispetto al piano dell’orbita
b) il moto della maggioranza avviene in senso antiorario
Il concetto di giorno nasce dal tempo impiegato a compiere un giro su se stessi.
L’irraggiamento e le stagioni
[figura 3 – l’irraggiamento e le stagioni]
La quantità di luce e calore ricevuta da un pianeta dipende in primo luogo dalla distanza dal sole; più è lontano e meno luce e calore riceve.
La dipendenza è quadratica cioè raddoppiando la distanza l’irraggiamento si riduce di 4 volte (4 = 22).
Questo spiega, in linea di massima, perchè i pianeti più vicini al sole sono più caldi e quelli più lontano più freddi.
[figura 4 – l’irraggiamento secondo l’inclinazione]
Localmente però l’irraggiamento ricevuto da ogni singola porzione del pianeta dipende dall’inclinazione con cui lo si riceve.
E’ massimo se lo si riceve a perpendicolo (nella figura 4 – nei pressi della linea più in basso), è nullo se lo si riceve completamente di lato (nei pressi della linea più in alto). La dipendenza esatta è la funzione trigonometrica coseno se il riferimento è la perpendicolare.
Questo effetto locale abbinato ad un asse di rotazione inclinato (come per la terra) risulta nelle varie stagioni.
La spiegazione è la seguente: riferendosi alla figura 3 (sopra), si consideri la terra di sinistra e si osservi che:
– tutto l’emisfero boreale (nord) è illuminato e contiene il punto di massimo irraggiamento che si trova sopra l’equatore di 23,5° (tanto quanto l’inclinazione dell’asse terrestre); come conseguenza si scalderà di più.
– l’emisfero australe (sud) è solo parzialmente illuminato (infatti i pressi del polo sud sono completamente al buio) e comunque riceve l’irraggiamento con forte inclinazione e quindi debolmente e si scalderà di meno.
Questa è la situazione che si ha durante la nostra (abitanti dell’emisfero boreale) estate. Nello stesso periodo è inverno per l’emisfero australe.
Viceversa sempre riferendosi alla figura 3, si consideri la terra di destra e si osservi che:
– tutto l’emisfero australe è illuminato e contiene il punto di massimo irraggiamento che si trova sotto l’equatore di 23,5°; come conseguenza si scalderà di più.
– l’emisfero boreale è solo parzialmente illuminato (i pressi del polo nord sono completamente al buio) e comunque riceve l’irraggiamento con forte inclinazione e quindi debolmente e si scalderà di meno.
Questa è la situazione che si ha durante il nostro inverno. Nello stesso periodo è estate per l’emisfero australe.
Tra le due situazioni sopra discusse, che per inciso sono i casi limite, ci sono anche situazioni intermedie che risultano nelle stagioni temperate (primavera ed autunno).
E’ bene ripetere che l’irraggiamento dipende anche dalla distanza dal sole. Questo è particolarmente significativo per i pianeti con orbite molto schiacciate (con grande eccentricità, ovvero che si allontanano molto da un cerchio) e che quindi si trovano a distanze considerevolmente diverse nei diversi punti dell’orbita come per esempio Mercurio.
Anche la Terra subisce un po’ questo effetto ed infatti le stagioni australi sono più estreme di quelle boreali.
Il motivo è che durante l’estate australe la terra è più vicina (e quindi sono concomitanti i due effetti maggior vicinanza e grande irraggiamento) e durante l’inverno australe più lontana (e quindi sono concomitanti i due effetti minor vicinanza e scarso irraggiamento).
Le stagioni boreali sono più temperate perchè invece i due effetti sono contrapposti (in estate minor vicinanza e grande irraggiamento ed in inverno maggior vicinanza e scarso irraggiamento).
Moto del baricentro
[figura 5 – il moto del baricentro]
Per i pianeti che hanno uno o più satelliti il moto su orbite ellittiche è solo un’approssimazione della realtà.
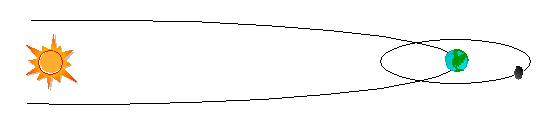
In effetti non è la terra che orbita intorno al sole ma è il sistema terra-luna che lo fa.
Si osservi la figura 5 e si consideri la terra e la luna di sinistra. E’ evidente che quando la luna si protende verso il sole (cioè si allinea con il sole e si avvicina ad esso) il baricentro del sistema terra-luna posizionato in un qualche punto tra il centro della terra e la luna stessa (in misura inversa delle due masse) causa uno spostamento della terra della stessa misura in direzione opposta al sole.
Viceversa considerando la terra e la luna di destra avviene esattamente il contrario poiché la luna si protende dalla parte opposta al sole e la nuova collocazione del baricentro del sistema terra-luna risulta in uno spostamento della terra in direzione del sole.
Ad un osservatore esterno il moto della terra parrebbe come l’insieme del moto orbitale “normale” sul quale si inserisce una modulazione armonica che la avvicina ed allontana dal sole.
Poiché la luna è un 81esimo della massa terrestre facendo i debiti calcoli risulta che il baricentro si sposta dal centro della terra di circa 4660 km ovvero il 73% del raggio terrestre. Si noti che una luna un po’ più grande o lontana avrebbe spostato il baricentro fuori dalla terra.
Quindi in generale non è un pianeta che orbita intorno al sole ma è il baricentro del sistema pianeta-satelliti che si muove attorno al sole su orbite ellittiche (si legga: con il sole in uno dei fuochi).
Moto attorno al sole?
[figura 6 – il sole]
Anche l’affermazione “moto attorno al sole su orbite ellittiche” è suscettibile di precisazione.
Il moto dei vari pianeti non è attorno al sole ma attorno al baricentro del sistema sole-pianeti (più satelliti, asteroidi, comete, ecc.) che si discosta dal centro del sole essendo influenzato dalla massa e dalla posizione di tutti i corpi.
La sola influenza di giove che vanta una massa di circa 1/1.000 di quella del sole ed orbita a 775 milioni di km da esso è sufficiente a portare il baricentro sole-giove al di fuori del sole stesso (circa 775.000 km dal centro del sole).
Altri moti?
In aggiunta a quanto già detto i pianeti partecipano ai moti:
a) del sole nell’interno della galassia e
b) della galassia rispetto al gruppo locale ed all’ammasso della vergine
Posizione dei pianeti interni
[figura 7 – posizione dei pianeti interni]
I pianeti inferiori sono sempre vicino al sole.
Il massimo allontanamento dal sole (elongazione) per mercurio è 28° e per venere 48°. Questi valori si ottengono quando mercurio e venere si trovano in prossimità del loro afelio (punto più lontano dal sole nell’orbita).
La situazione in cui il sole è da una parte ed il pianeta dall’altra rispetto alla terra, situazione detta di opposizione, è impossibile per i pianeti inferiori (perchè la loro orbita è più piccola di quella terrestre).
[figura 8 – la congiunzione inferiore e superiore di venere]
Riferendosi alla figura 8 si analizzi il moto di venere.
Partendo dalla posizione di minima distanza dalla terra, detta di congiunzione inferiore, (figura di sinistra), in cui il pianeta è allineato col sole e quindi difficilmente osservabile, venere si allontana dal sole muovendosi di moto retrogrado (contrario al moto normalmente osservato dai vari corpi celesti cioè da est ad ovest) fino a raggiungere la massima elongazione occidentale (circa 1/4 dell’orbita). In questa fase appare al mattino ed è chiamato lucifero.
Dopo un periodo di stazionamento (in cui appare apparentemente fermo), con moto diretto, si avvicina rapidamente al sole diventando sempre più piccolo fino a raggiungere la congiunzione superiore, punto in cui è alla massima distanza dalla terra ed essendo ancora allineato col sole difficilmente osservabile.
Riappare quindi a oriente, è osservabile alla sera ed è chiamato vespero, fino a raggiungere la massima elongazione orientale (circa 3/4 dell’orbita).
Segue un altro stazionamento poi con moto retrogrado si riavvicina al sole e torna alla posizione di congiunzione inferiore.
Il moto di mercurio è simile.
Posizione dei pianeti esterni
[figura 9 – posizione dei pianeti esterni – congiunzione ed opposizione]
I pianeti superiori possono assumere una qualunque posizione rispetto alla terra.
L’allineamento di un pianeta con il sole si definisce congiunzione (il pianeta ed il sole sono dalla stessa parte).
La situazione opposta opposizione (il pianeta è da una parte ed il sole dall’altra).
[figura 10 – posizione dei pianeti esterni – quadrature]
Se il pianeta forma un angolo retto col sole si parla di quadratura.
La meccanica celeste
Le leggi che regolano il moto dei pianeti (e non solo) sono:
a) la legge di gravitazione (di Newton)
f=Gm1m2/d2
Questa legge dice in sostanza che la materia attira altra materia (si pensi che ogni oggetto attira ed è attirato da ogni altro oggetto) con una forza che dipende in modo diretto dalle masse coinvolte (più grandi gli oggetti più grande la forza) ed in modo inverso dalla distanza al quadrato (più distanti gli oggetti più debole la forza, e siccome la distanza compare al quadrato raddoppiando la distanza la forza diventa 1/4 che è il quadrato di 1/2).
b) le leggi di Keplero
1) le orbite dei pianeti sono ellissi con il sole posto in uno dei fuochi
E’ la più conosciuta delle tre. Le orbite dei corpi celesti sono delle coniche (curve che si ottengono sezionando un cono: ellissi, parabole ed iperboli) e più normalmente ellissi (che è l’unica delle tre ad essere una curva chiusa e che quindi permette un moto ripetitivo nel tempo). Le ellissi sono quindi come dei cerchi schiacciati ma, si badi bene il sole non occupa il centro della figura ma una posizione speciale, scostata dal centro lungo l’asse maggiore, corrispondente ad uno dei due fuochi).
2) il raggio vettore sole-pianeta descrive aree uguali in tempi uguali
Questa legge si traduce nel fatto che il pianeta si muove lungo l’orbita con velocità variabile. Più veloce al perielio e più lento all’afelio.
3) T2/R3=k …=4o2/G(m1+ m2)
La prima formula scoperta empiricamente da keplero si traduce nel fatto che aumentando la dimensione dell’orbita deve anche aumentare il tempo necessario a percorrerla (con una relazione un po’ più complessa dovuta alle varie potenze che compaiono).
La seconda parte completa con il contributo di Newton questa relazione dimensione asse maggiore e tempo di percorrenza con le masse in gioco (sole e pianeta).
Dalla terza legge di Keplero si può ricavare la massa del sole.
Dalla formula T2/R3=4o2/G(m1+ m2), trascurando la massa terrestre rispetto a quella del sole (T2/R3=4o2/Gm) si ottiene m=4o2 R3/G T2 =2×1033g ovvero 2×1027t, cioè 2 miliardi di miliardi di miliardi di tonnellate.
La massa della terra si può ricavare dalla sua gravità g=Gm/r da cui m=gr/G =6×1027g ovvero 6×1021 t, cioè 6 mila miliardi di miliardi di tonnellate.
Caratteristiche orbitali
La tabella che segue mostra:
a) le distanze dei vari pianeti dal sole espresse in u.a. (unità astronomica = distanza terra sole media = 149.600.00 km)
b) l’inclinazione dei piani orbitali dei vari pianeti (con riferimento al piano terrestre detto eclittica)
c) l’eccentricità dell’orbita (cioè quanto l’ellisse è schiacciata)
| Distanza | Inclinazione | Eccentricità | |
| Mercurio | 0,29 | 7,0 | 0,206 |
| Venere | 0,72 | 3,4 | 0,007 |
| Terra | 1,00 | 0 | 0,017 |
| Marte | 1,52 | 1,9 | 0,093 |
| Giove | 5,20 | 1,3 | 0,048 |
| Saturno | 9,54 | 2,5 | 0,056 |
| Urano | 19,18 | 0,8 | 0,047 |
| Nettuno | 30,06 | 1,8 | 0,009 |
| Plutone | 39,44 | 17,3 | 0,247 |
[tabella 1 – caratteristiche orbitali dei pianeti – distanza, inclinazione ed eccentricità dell’orbita]
La legge di Titius-Bode
Tempo fa, quando l’universo conosciuto terminava con saturno, alcuni studiosi notarono che le distanze dei vari pianeti dal sole si potevano esprimere con una formula empirica (nota come legge di Titius-Bode). Secondo questa formula c’era un posto vacante tra marte e giove; ovvero ci si aspettava ci fosse un pianeta intermedio tra di essi. Ci fu un’accanita ricerca che portò alla scoperta di Cerere e si pensò con questo di avere completato il quadro che la legge forniva.
Ma in breve vennero scoperti altri corpi (Pallade, Vesta, Giunone ecc.) e si capì che il posto del quarto pianeta era di fatto occupato da una moltitudine di corpi celesti che vennero chiamati pianetini o asteroidi. Oggi se ne conoscono migliaia.
La maggioranza dei pianeti orbita su piani pressoché coincidenti con l’eclittica. Se ne discostano in modo significativo mercurio ed ancor più plutone.
Anche l’eccentricità è mediamente piccola (cioè l’orbita è vicina ad un cerchio). Se ne discostano marte, ed ancor più mercurio plutone.
La tabella che segue mostra:
a) i tempi di rivoluzione dei vari pianeti (espressi in anni) e
b) i tempi di rotazione dei vari pianeti (espressi in giorni)
| Rivoluzione | Rotazione | |
| Mercurio | 0,24 | 58,667 |
| Venere | 0,62 | -243 |
| Terra | 1 | 1 |
| Marte | 1,88 | 1,025 |
| Giove | 11,86 | 0,408 |
| Saturno | 29,46 | 0,425 |
| Urano | 84,01 | -0,65 |
| Nettuno | 164,79 | 0,766 |
| Plutone | 247,7 | 6,375 |
[tabella 2 – caratteristiche orbitali dei pianeti – rivoluzione e rotazione]
Coerentemente con la terza legge di Keplero i tempi di rivoluzione crescono dal pianeta più vicino, mercurio che compie circa 4 giri in un nostro anno, progressivamente fino al più lontano plutone che compie circa 4 giri in un millennio.
I giganti gassosi ruotano tutti molto velocemente e giove, tra di essi, è in assoluto il più veloce.
Marte ha un giorno molto simile al nostro.
Mercurio e venere hanno un giorno eccezionalmente lungo comparabile con la lunghezza del loro anno.
Venere ed urano ruotano con moto retrogrado (orario).
Gli elementi orbitali
Gli elementi orbitali sono quell’insieme di informazioni necessarie a definire l’orbita di un pianeta (od altro corpo celeste) nello spazio.
E’ necessario definire:
a) la forma dell’orbita
b) il piano su cui giace l’orbita
c) l’orientamento dell’orbita sul piano
d) gli elementi temporali
[figura 11 – elementi orbitali – la forma dell’orbita]
Definizione della forma dell’orbita
Per definire la forma dell’orbita bastano due dati:
a) a – la dimensione del semiasse maggiore
b) e – l’eccentricità (e=c/a; c è la distanza focale)
[figura 12 – elementi orbitali – definizione del piano dell’orbita ed orientamento dell’orbita sul piano]
Definizione del piano dell’orbita
Per definire il piano dell’orbita bastano due dati:
i – angolo del piano (riferimento eclittica)
W – angolo della linea dei nodi (riferimento c)
Definizione dell’orientamento dell’orbita sul piano
Per definire l’orientamento dell’orbita sul piano basta un dato:
z – angolo del perielio (riferimento linea dei nodi)
Definizione degli elementi temporali
P – periodo rivoluzione (non necessario perchè ricavabile da a = semiasse maggiore con la terza legge di Keplero)
T0 -passaggio al perielio
Equinozi e solstizi
[figura 13 – equinozi e solstizi]
Ci sono alcuni punti notevoli dell’orbita terrestre che sono i solstizi e gli equinozi.
Le considerazioni che seguono e le date riportate valgono per l’emisfero boreale.
Per l’emisfero australe questi eventi vanno riconsiderati e le date spostate di 1/2 anno.
[figura 14 – alba del solstizio d’estate – Milano]
Il solstizio d’estate (intorno al 21 giugno) è il giorno in cui il sole raggiunge la massima altezza. Ne consegue il giorno più lungo.
[figura 15 – alba del solstizio d’inverno – Milano]
Il solstizio d’inverno (intorno al 21 dicembre) è il giorno in cui il sole raggiunge la minima altezza. Ne consegue il giorno più corto.
[figura 16 – alba dell’equinozio di primavera – a latitudine 0°, Milano, latitudine 90°]
L’equinozio di primavera (intorno al 20 marzo) è il giorno in cui il sole passa dall’emisfero australe al boreale.
In quel giorno i meridiani e gli equatori celesti ed eclitticali coincidono in un unico punto (c).
Nota: Si ricordi che il sistema di posizionamento celeste è una proiezione nello spazio del sistema terrestre. In questo sistema l’equatore celeste è la proiezione dell’equatore terrestre ed i meridiani celesti sono una proiezione dei meridiani terrestri. Questo sistema è inclinato rispetto all’eclittica di 23,5° come l’asse terrestre.
Nel sistema di riferimento eclitticale l’equatore eclitticale coincide con l’eclittica ed i vari meridiani sono perpendicolari ad essa.
Il sole sorge esattamente ad est e tramonta esattamente ad ovest.
Inizia il giorno al polo nord (e la notte al polo sud).
Il giorno e la notte hanno circa la stessa durata.
[[figura 17 – alba dell’equinozio d’autunno – a latitudine 0°, Milano, latitudine 90°]
L’equinozio d’autunno (intorno al 22 settembre) è il giorno in cui il sole passa dall’emisfero boreale all’australe.
In quel giorno i meridiani e gli equatori celesti ed eclitticali coincidono in un unico punto (z).
Il sole sorge esattamente ad est e tramonta esattamente ad ovest.
Inizia il giorno al polo sud (e la notte al polo nord).
Il giorno e la notte hanno circa la stessa durata.
Il moto di precessione
[figura 18 – il moto di precessione]
L’attrazione gravitazionale della luna e del sole sulla terra che non è una sfera perfetta ma un ellissoide panciuto genera una forza che tende a raddrizzare l’asse terrestre.
La reazione dinamica a questa forza è una rotazione lentissima (~25.765 anni) dell’asse terrestre noto come moto di precessione lunisolare.
Il moto e’ in senso orario, ampiezza 50,3″ anno.
Nutazione
La nutazione è un moto, costituito da una piccola oscillazione (ampiezza massima 18,4″), che si sovrappone al moto di precessione.
E’ causato dal fatto che l’attrazione della luna non giace sull’eclittica essendo l’orbita lunare spostate di circa 5°.
Ha un periodo di 18,6 anni; lo stesso dei nodi lunari.
La rotazione degli apsidi
[figura 19 – la rotazione della linea degli apsidi terrestre]
La linea che congiunge il perielio e l’afelio (asse maggiore) è detta linea degli apsidi.
Essa ruota di 11,6″ anno in senso antiorario effettuando un giro completo in 117.000 anni.
Come conseguenza la longitudine del perielio si sposta rispetto all’equinozio di 61,9″ (50,3+11,6) all’anno.
Si noti che lo spostamento del perielio modifica la durata delle stagioni.
Variazione dell’inclinazione dell’asse
[figura 20 – variazione dell’inclinazione dell’asse terrestre]
L’asse terrestre varia la sua inclinazione nell’arco di 40.0000 anni tra un minimo di 21° 55′ ed un massimo di 24° e 20′.
Questo moto è irregolare e ci può essere una inversione prima di aver raggiunto un estremo.
Attualmente il valore è 23° 27′ in diminuzione.
L’inclinazione dell’asse influenza il clima.
Polodia
[figura 21 – la polodia]
La terra non è un corpo omogeneo e nel suo interno le masse non sono distribuite in modo perfettamente uniforme.
Il risultato è che il centro di gravità non coincide con l’asse di rotazione.
Pertanto i poli, che dovrebbero essere fermi, sono animati da un moto di oscillazione irregolare (polodia) che li sposta continuamente entro una ventina di metri.
Variazione dell’eccentricità
[figura 22 – variazione dell’eccentricità dell’orbita terrestre]
Ed infine la terra è soggetta ad un lento movimento che cambia le distanze tra i fuochi tra un minimo di
Attualmente la distanza è
Le dimensioni degli assi sono rispettivamente 152.100.000 e
L’orbita terrestre e le stagioni
[figura 23 – l’orbita terrestre e le stagioni]
La figura 23 mostra che la linea degli apsidi è inclinata di circa 12° rispetto alla linea dei solstizi. Questo fatto, non molto conosciuto, ha interessanti conseguenze:
1) il punto di minima distanza dal sole non coincide con il solstizio d’inverno. Il perielio infatti avviene il 3 gennaio e non il 22 dicembre. E similmente il punto di massima distanza dal sole non coincide con il solstizio d’estate. L’afelio infatti avviene il 4 luglio e non il 21 giugno.
Le date 3 gennaio e 4 luglio cambiano lentamente col tempo per effetto della rotazione degli apsidi.
2) i confini delle stagioni non coincidono col perielio ed afelio ne con la loro perpendicolare.
3) quanto espresso nei punti 1) e 2) ed il fatto che la velocità della terra vari durante l’orbita (in accordo alla 2° legge di keplero) causa stagioni di lunghezza diversa e non uguali tra loro, ne uguali a due a due (vedi tabella sotto).
La velocità della terra è massima al perielio (61’/giorno) ed è minima all’afelio (57’/g).
Anche la grandezza apparente del sole varia tra 31′,6 (4 luglio) e 32′,6 (3 gennaio).
| giorni | ore | |
| Primavera | 92g | 21h |
| Estate | 93g | 14h |
| Autunno | 89g | 18h |
| Inverno | 89g | 01h |
[tabella 3 – durata delle stagioni]
L’anno
[figura 24 – l’anno]
L’anno è il tempo impiegato dalla terra a compiere un giro attorno al sole.
Questa definizione è conosciuta da tutti ma l’astronomo differenzia diversi tipi di anni con durate diverse in funzione della scelta di un riferimento diverso.
Si definiscono quindi:
anno siderale: il tempo impiegato dalla terra a compiere un giro intorno al sole e riallinearsi con una stella
è l’anno così come percepito da un osservatore lontano.
anno tropico: il tempo impiegato dalla terra a compiere un giro intorno al sole e riallinearsi con il punto equinoziale vernale
è l’anno sul quale si basano le stagioni ed è l’anno ufficiale per l’umanità. E’ più corto dell’anno siderale per effetto della precessione degli equinozi.
anno anomalistico: il tempo impiegato dalla terra a compiere un giro intorno al sole e riallinearsi con il perielio dell’orbita
è più lungo dell’anno siderale per effetto della rotazione della linea degli apsidi che causa uno spostamento del perielio in avanti.
anno draconico: il tempo impiegato dalla terra a compiere un giro intorno al sole e riallinearsi con il nodo ascendente dell’orbita lunare
è diverso dagli altri perchè il riferimento è legato al moto della luna.
durata:
| giorni | ore | minuti | secondi | |
| siderale | 365 | 06 | 09 | 09 |
| tropico | 365 | 05 | 48 | 46 |
| anomalistico | 365 | 06 | 13 | 54 |
| draconico | 346 | 14 | 03 |
[tabella 4 – durata degli anni astronomici]
comparata con:
| giorni | ore | minuti | secondi | |
| Giuliano | 365 | 06 | ||
| Gregoriano | 365 | 05 | 49 | 12 |
[tabella 5 – durata degli anni civili giuliano e gregoriano]
Nota: il calendario giuliano fu istituito da Giulio Cesare nel 45 a.C. e consisteva in un ciclo di quatto anni, di cui tre anni normali (di 365 giorni) ed uno bisestile (di 366 giorni). L’anno giuliano durava quindi 365,25 giorni (365 + 1/4).
Il calendario gregoriano fu istituito da papa Gregorio XIII nel 1582 sopprimendo gli anni bisestili centenari ma lasciando i quadricentenari con il risultato di avere 97 anni bisestili ogni 400 anni. L’anno gregoriano durava e dura tuttora 365,2425 giorni (365 + 97/400).
Come si nota dalle tabelle 4 e 5 sopra la durata dell’anno gregoriano è in eccesso di 26 secondi rispetto all’anno ufficiale (tropico).
Il moto della luna
[figura 25 – il moto della luna]
La luna si muove intorno alla terra su un’orbita ellittica, in senso antiorario (diretto).
Il periodo rivoluzione e rotazione coincidono e sono di 27,3216 giorni,. Per questa ragione la luna mostra sempre la stessa faccia.
L’eccentricità dell’orbita è 0,0549.
La distanza dalla terra è: media
Il raggio lunare
La massa lunare è 7,35×1025g (1/81,3 terra) ovvero 7,35×1019t cioè 73,5 miliardi di miliardi di tonnellate.
L’inclinazione dell’asse di rotazione è 6,7°.
La rotazione della linea dei nodi
[figura 26 – la rotazione della linea dei nodi dell’orbita lunare]
Il piano dell’orbita lunare è inclinato di 5° 9′ rispetto all’eclittica.
L’intersezione tra il piano dell’orbita lunare e l’eclittica (linea dei nodi) ruota in senso orario in 6793 giorni pari a 18,6 anni (moto detto di retrogradazione dei nodi).
La rotazione della linea degli apsidi
[figura 27 – la rotazione della linea degli apsidi lunare]
La linea degli apsidi (che congiunge il perigeo e l’apogeo) ruota in senso antiorario effettuando un giro completo in 8,85 anni.
Altre irregolarità
Vi sono altre irregolarità del moto lunare dovute a perturbazioni esercitate dal sole:
l’evezione: è una irregolarità del moto in longitudine dovuta alla variazione dell’eccentricità dell’orbita lunare (31,8 anni)
la variazione: è una ineguaglianza della velocità della luna (con periodo metà mese sinodico)
l’equazione annua: è un’altra ineguaglianza della velocità lunare (con periodo anno anomalistico)
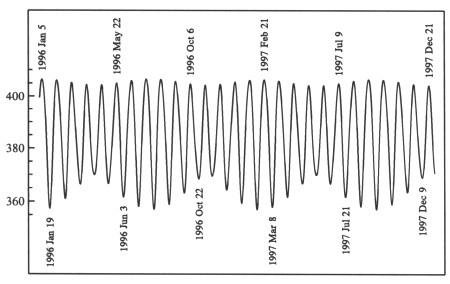
[figura 28 – andamento della distanza lunare – variazioni del perigeo ed apogeo]
L’orbita lunare viene stirata quando si allinea con il sole.
Ne risulta una distanza variabile al perigeo ed apogeo in funzione della posizione.
La declinazione della luna
L’orbita lunare è inclinata di 5,1° rispetto all’eclittica che è a sua volta inclinata di 23,5° rispetto all’equatore
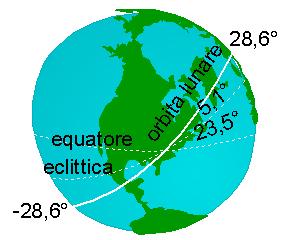
[figura 29 – la declinazione della luna – nodo ascendente in fase con punto c]
Come conseguenza della retrogradazione dei nodi la line dei nodi può assumere qualsiasi orientamento sull’eclittica.
Quando casualmente la linea dei nodi è allineata col punto c ed il nodo coincidente è quello ascendente le due inclinazioni (quella dell’orbita lunare rispetto all’equatore terrestre e quella dell’equatore rispetto all’eclittica) si sommano e la luna raggiunge una declinazione di 28,6° (23,5+5,1=28,6). Dopo mezza lunazione (circa 15 giorni) la declinazione sarà -28,6°.
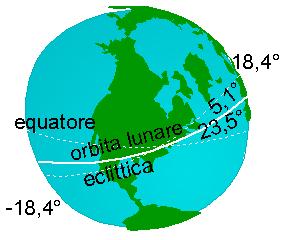
[figura 30 – la declinazione della luna – nodo discendente in fase con punto c]
Circa 9,3 anni dopo (mezzo ciclo di retrogradazione dei nodi, 18,6:2=9,3) sarà il nodo discendente a coincidere col punto c ed in questo caso le due inclinazioni si sottraggono e la luna raggiunge una declinazione di 18,4° (23,5-5,1=18,4). ed ancora dopo mezza lunazione la declinazione sarà -18,4°.
La librazione
I tempi di rotazione e rivoluzione della luna sono gli stessi. La conseguenza è che noi dovremmo vedere sempre la stessa faccia.
Un esame accurato evidenzia però che si può osservare più del 50% della superficie lunare (in effetti si arriva al 59%).
Ciò è dovuto alla librazione lunare che è di due tipi: fisica ed ottica
a) fisica – è dovuta alla non perfetta distribuzione delle masse (mascons) che causa una oscillazione dell’asse di rotazione
b) ottica – si divide a sua volta in:
in latitudine – causata dal fatto che la luna nel compiere la propria orbita sta un po’ sotto ed un po’ sopra l’eclittica permettendo quindi di scorgere una porzione maggiore dell’emisfero meridionale prima e settentrionale poi
in longitudine – dovuta alla diversa velocità di rivoluzione (mentre la rotazione è costante) permettendo di vedere in certi momenti in po’ di più ad oriente ed in altri ad occidente
diurna – dovuta alla variazione di prospettiva tra quando è all’orizzonte ed alta nel cielo.
Il mese
[figura 31 – il mese lunare]
Il concetto di mese nasce dal moto della luna
In funzione del riferimento scelto si definiscono:
mese siderale: il tempo impiegato dalla luna a compiere un giro intorno alla terra e ritornare in congiunzione con una stella
è il mese così come percepito da un osservatore lontano.
mese sinodico: il tempo impiegato dalla luna a compiere un giro intorno alla terra e ritornare in congiunzione con il sole
è il mese così come percepito da un osservatore sulla terra.
mese anomalistico: il tempo impiegato dalla luna a compiere un giro intorno alla terra e ritornare in congiunzione con il perigeo dell’orbita
mese draconico: il tempo impiegato dalla luna a compiere un giro intorno alla terra e ritornare in congiunzione con il suo nodo ascendente
mese tropico: il tempo impiegato dalla luna a compiere un giro intorno alla terra e ritornare in congiunzione con il punto equinoziale vernale
durata:
| giorni | ore | minuti | secondi | |
| Siderale | 27 | 07 | 43 | 12 |
| Sinodico | 29 | 12 | 44 | 03 |
| Anomalistico | 27 | 13 | 18 | 37 |
| Draconico | 27 | 05 | 05 | 36 |
| Tropico | 27 | 07 | 43 | 05 |
[tabella 6 – durata dei mesi lunari astronomici]
Armonie dei moti
In alcune circostanze i moti dei vari corpi celesti producono l’equivalente di certe importanti assonanze musicali.
Per esempio la rotazione e rivoluzione della luna avvengono nello stesso tempo quindi sono fenomeni con la stessa frequenza equivalenti al suonare la stessa nota (es. do3-do3).
Le rivoluzioni di plutone e nettuno stanno in rapporto 2 e 3 (ovvero ogni due rivoluzioni di plutone nettuno ne fa tre) come in un rapporto di quinta (es. do3-sol3)
Le rivoluzioni di saturno e giove stanno in un rapporto di un’ottava più una terza maggiore (es. do3-mi4).
La rivoluzione e la rotazione di mercurio stanno in rapporto 2 e 3 come in un rapporto di quinta (es. do3-sol3).
I pianeti troiani ruotano in sincronismo con giove e quindi sono equivalenti al suonare la stessa nota (es. do3-do3).
I primi tre satelliti di giove ruotano con periodo doppio rispetto al precedente quindi come un rapporto musicale di ottava (es. do2-do3-do4).
La rivoluzione di caronte è sincrona con la rotazione di plutone. Ancora equivalenti a suonare la stessa nota.
Altre armonie potrebbero essere ancora da scoprire.
Bibliografia
Libri
| Titolo | Autore | Editore |
| Introduzione all’Astronomia | Giuliano Romano | Franco Muzzio & c. |
| Calendario | David Ewing Duncan | Piemme Pocket |
| L’Universo | De Agostini |